设计一个递归算法求解汉诺塔问题
算了好久 囧
-
#include<iostream>
-
using namespace std;
-
-
void move(int n, int x, int y){
-
static int t = 1;
-
cout<<"第"<<t++<<"步 "<<char(x+64)<<"(第"<<n<<"号盘子) -> "<<char(y+64)<<endl;
-
}
-
-
void hanoi(int n,int a, int b, int c){
-
if(n==1)
-
move(1,a,c);
-
else{
-
hanoi(n-1,a,c,b);
-
move(n,a,c);
-
hanoi(n-1,b,a,c);
-
}
-
}
-
-
int main(){
-
int n;
-
-
cout<<"请输入第一根柱子上的盘子数:";
-
cin>>n;
-
-
hanoi(n,1,2,3);
-
-
return 0;
-
}
用递归算法重新设计选择排序算法
不知道是不是这样写 囧?
-
#include<iostream>
-
using namespace std;
-
-
#define N 100
-
-
void sort(int A[], int n){
-
if(n==1)return;
-
for(int i=0; i<n-1; i++){
-
if(A[i]>A[n-1]){
-
int t = A[i];
-
A[i] = A[n-1];
-
A[n-1] = t;
-
}
-
}
-
sort(A,n-1);
-
}
-
-
void print(int A[], int n){
-
for(int i=0; i<n; i++){
-
cout<<A[i]<<" ";
-
}
-
cout<<endl;
-
}
-
-
int main(){
-
int A[N], n;
-
-
input:
-
cout<<"请输入数组的长度(<"<<N<<"):";
-
cin>>n;
-
-
if(n<=0){
-
cout<<"n必须大于0!"<<endl;
-
goto input;
-
}
-
if(n>=N){
-
cout<<"n必须小于"<<N<<"!"<<endl;
-
goto input;
-
}
-
-
cout<<"请输入数组的元素:";
-
for(int i=0; i<n; i++){
-
cin>>A[i];
-
}
-
-
cout<<"排序前的数组:";
-
print(A,n);
-
-
sort(A,n);
-
-
cout<<"排序后的数组:";
-
print(A,n);
-
-
return 0;
-
}
用递归算法求解f(x)=x-x^3/3!+x^5/5!-x^7/7!+...
用递归算法求解如下问题,计算到第n项为止:
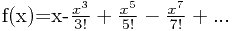
用递归算法求解f(x)=x/2+x^2/4+...+x^n/2^n
用递归算法求解如下问题:
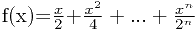
设计一个递归算法计算Fibonacci数列
囧 好久没写算法了……
-
#include<iostream>
-
using namespace std;
-
-
int getFibonacci(int n){
-
if(n==0||n==1)return 1;
-
return getFibonacci(n-1)+getFibonacci(n-2);
-
}
-
-
int main(){
-
int n;
-
-
while(true){
-
cout<<"请输入要求的Fibonacci数列项数(输入-1退出):";
-
cin>>n;
-
if(n<0)break;
-
-
cout<<"第"<<n<<"项是:";
-
cout<<getFibonacci(n)<<endl;
-
}
-
-
return 0;
-
}
【模板】Prim - 最小生成树
我最常用的最小生成树算法 = 3=
-
#define N 505
-
#define MAX 65540
-
-
int n;
-
int edge[N][N];
-
int sum;
-
-
void prim(){
-
int i,j,k;
-
int lowcost[N];
-
bool visit[N]={false};
-
sum = 0;
-
for (i=0;i<n;i++){
-
lowcost[i]=edge[0][i];
-
}
-
visit[0]=true;
-
for (i=1;i<n;i++){
-
j=0;
-
while(visit[j]) j++;
-
for (k=0;k<n;k++)
-
if((!visit[k])&&(lowcost[k]<lowcost[j])) j=k;
-
sum = lowcost[j]>sum?lowcost[j]:sum;
-
visit[j]=true;
-
for (k=0;k<n;k++)
-
if (!visit[k]&&(edge[j][k]<lowcost[k])){
-
lowcost[k]=edge[j][k];
-
}
-
}
-
}
没连通的边长应为MAX。
求最大生成树时为0,修改两个小于号即可。
结点是从0到N。
【模板】SPFA - 单源最短路径
看了wekooo给的某论文,从里面pascal翻过来 = =
-
void SPFA(int s){
-
for(int i=1;i<=n;i++){
-
d[i] = MAX;
-
}
-
int queue[N*N] = {0};
-
bool visit[N] = {false};
-
int front = 0, rear = 1;
-
//int path[N];
-
queue[front] = s; visit[s] = true; d[s] = 0;
-
while(front<rear){
-
int u = queue[front];
-
visit[u] = false;
-
for(int i=1; i<=n; i++){
-
if (d[i]>d[u]+ edges[u][i]){
-
d[i]= d[u]+edges[u][i];
-
//path[i] = u;
-
if( !visit[i] ){
-
visit[i] = true;
-
queue[rear++] = i;
-
}
-
}
-
}
-
front++;
-
}
-
}
调用时,初始结点s,目标结点e,则
SPFA(s);
cout<<d[e]<<endl;
即可。
注意结点是从1存储到N。
不能连通时值为MAX。
【模板】Dijkstra - 单源最短路径
当年整理得 - -
-
#define N 1002
-
#define MAX 99999
-
int edges[N][N],d[N],n;
-
-
void dijkstra(int v)
-
{
-
int i,j;
-
bool s[N]={false};
-
for(i=1;i<=n;i++)
-
d[i]=edges[v][i];
-
d[v]=0;s[v]=true;
-
for(i=1;i<n;i++)
-
{
-
int temp=MAX;
-
int u=v;
-
for(j=1;j<=n;j++)
-
if((!s[j])&&(d[j]<temp))
-
{
-
u=j;
-
temp=d[j];
-
}
-
s[u]=true;
-
for(j=1;j<=n;j++)
-
if((!s[j])&&(edges[u][j]<MAX)&&(d[u]+edges[u][j])<d[j])
-
d[j]=d[u]+edges[u][j];
-
}
-
-
}
调用时,初始结点s,目标结点e,则
dijkstra(s);
cout<<d[e]<<endl;
即可。
注意结点是从1存储到N。
不能连通时值为MAX。
