Liny_@NotePad

沉迷ACG中

字符串匹配的RK算法+随机

在使用RK算法进行字符串匹配时，q必须是一个充分大的素数。为了减少出现假匹配的概率，先计算小于12mn2的素数集合，再从集合中随机取出一个素数，可使假匹配的概率小于1/n。此外，这个算法总能得到正确的答案。

  1. #include<iostream>
  2. #include<map>
  3. #include<set>
  4. #include<time.h>
  5. using namespace std;
  6.  
  7. #define N 100   // 待匹配串的最多长度
  8. #define M 20    //  模式串的最多长度
  9.  
  10. #define MULTIPLIER 0x015A4E35L
  11. #define INCREMENT 1
  12.  
  13. static unsigned long seed;
  14.  
  15. /*      生成随机数种子 */
  16. void random_seed(unsigned long d){
  17.         if(d==0){
  18.                 seed = time(0);
  19.         }else{
  20.                 seed = d;
  21.         }
  22. }
  23.  
  24. /*      生成一个low~high范围内的随机数 */
  25. unsigned int random(unsigned long low, unsigned long high){
  26.         seed = MULTIPLIER * seed + INCREMENT;
  27.         return ((seed>>16)%(high-low)+low);
  28. }
  29.  
  30. long BASE;                  //    进制数
  31. set<char> v;        //  存放待匹配串和模式串中出现的字符的集合
  32. map<char, int>data;     //   存放待匹配串和模式串中出现的字符的哈希表
  33.  
  34. /*      将串中出现的字符放入集合 */
  35. void inSet(char s[]){
  36.         int n = strlen(s);
  37.  
  38.         for(int i = 0; i<n; i++){
  39.                 v.insert(s[i]);
  40.         }
  41.  
  42.         BASE = v.size();
  43. }
  44.  
  45. /*      计算出现的字符的哈希表 */
  46. void countMap(){
  47.         data.clear();
  48.         int i = 0;
  49.         for(set<char>::iterator iter = v.begin(); iter!=v.end(); iter++){
  50.                 data[*iter] = i++;
  51.         }
  52. }
  53.  
  54. /*      出现的字符的哈希函数 */
  55. int ch(char s){
  56.         return data[s];
  57. }
  58.  
  59. /*
  60. * 字符串匹配
  61. * 输入：存放待匹配串的数组S[]，待匹配串的长度n，
  62. *             存放模式串的数组P[]，模式串的长度m，素数p
  63. * 输出：与P相匹配的子串在待匹配串中的起始位置loc
  64. */
  65. void match(char S[], long n, char P[], long m, long &loc, long q){
  66.         long b = BASE;
  67.         long i, k;
  68.         long w = 0, p = 0;
  69.         long x = 1;
  70.  
  71.         //      计算b^(m-1) % q
  72.         for(i=0; i<m-1; i++){
  73.                 x = (x*b)%q;
  74.         }
  75.  
  76.         //      计算第一个窗口子串的哈希值
  77.         for(i=0; i<m; i++){
  78.                 w = (w*b + ch(S[i]))%q;
  79.         }
  80.  
  81.         //      计算模式串的哈希值
  82.         for(i=0; i<m; i++){
  83.                 p = (p*b + ch(P[i]))%q;
  84.         }
  85.  
  86.         i = 0;
  87.         while((i<=n-m) && (loc == -1)){
  88.                 if(w==p) {      //    如果与模式串相等 则仔细检查是否真的相等
  89.                         for( k=0; k<m; k++){
  90.                                 if(S[i+k]!=P[k])break;
  91.                         }
  92.                         if(k>=m) loc = i;
  93.                 }
  94.                 //      计算下一个窗口子串的哈希值
  95.                 w = w - ch(S[i])*x%q;
  96.                 if(w<0) w += q;
  97.                 w = (w*b + ch(S[i+m]))%q;
  98.                 i++;
  99.         }
  100. }
  101.  
  102. /*
  103. * 字符串匹配的随机算法
  104. * 输入：存放待匹配串的数组S[]，待匹配串的长度n，
  105. *             存放模式串的数组P[]，模式串的长度m，
  106. *             小于12*m*n*n的素数集合R[]，素数集合的元素个数a
  107. * 输出：与P相匹配的子串在待匹配串中的起始位置loc
  108. */
  109. void match_random(char S[], long n, char P[], long m, long &loc, long R[], int a){
  110.         long q;
  111.         random_seed(0);
  112.         q = random(a/2,a);      //    从a/2~a范围中取一个素数
  113.         q = R[q];
  114.         match(S, n, P, m, loc, q);
  115. }
  116.  
  117. /*
  118. * 找素数算法
  119. * 输入：所找素数的上界size
  120. * 输出：所找素数集合的大小a
  121. */
  122. long* findPrime(int size, int &a){
  123.         long* r = new long[size];
  124.         bool* prime = new bool[size];
  125.        
  126.         int i,j;
  127.         prime[0] = false;
  128.         for(i=1; i<size; i++){
  129.                 prime[i] = true;
  130.         }
  131.  
  132.         i = 1;
  133.         while(i<size){
  134.                 if(prime[i]){
  135.                         j = (i+1)*2;
  136.                         while(j<size){
  137.                                 prime[j-1] = false;
  138.                                 j += i+1;
  139.                         }
  140.                 }
  141.                 i++;
  142.         }
  143.  
  144.         a = 0;
  145.         for(i=1; i<size; i++){
  146.                 if(prime[i-1]){
  147.                         r[a++] = i;
  148.                 }
  149.         }
  150.  
  151.         delete prime;
  152.  
  153.         return r;
  154. }
  155.  
  156. int main(){
  157.         char str[N], substr[M];
  158.  
  159.         while(cin>>str){
  160.                 if(!strcmp(str,"exit"))break;   // 待匹配串为exit时退出
  161.                 cin>>substr;
  162.  
  163.                 long loc = -1;
  164.                 int n = strlen(str);
  165.                 int m = strlen(substr);
  166.                 int a;
  167.                 long* R = findPrime(12*m*n*n, a);       //     计算小于12*m*n*n的素数集合
  168.  
  169.                 /* 计算待匹配串和模式串中出现的元素集合 */
  170.                 v.clear();
  171.                 inSet(str);
  172.                 inSet(substr);
  173.                 countMap();
  174.  
  175.                 //      随机匹配
  176.                 match_random(str, n, substr, m, loc, R, a);
  177.  
  178.                 if(loc==-1){    //  如果未匹配 则尝试用最接近12*m*n*n的素数进行匹配
  179.                         cout<<"No Found!"<<endl;
  180.                         match(str, n, substr, m, loc, R[a-1]);
  181.                         cout<<"Use Prime: "<<R[a-1]<<endl;
  182.                         if(loc==-1){
  183.                                 cout<<"No Found!"<<endl;
  184.                         }else{
  185.                                 cout<<"Location In "<<loc+1<<endl;
  186.                         }
  187.                 }else{
  188.                         cout<<"Location In "<<loc+1<<endl;
  189.                 }
  190.  
  191.                 delete R;
  192.                
  193.                 system("pause");
  194.                 cout<<"================================"<<endl;
  195.         }
  196.  
  197.         return 0;
  198. }

才知道%对负数不起作用……还需要自己手工判断……

【算法】与【数据结构】 RK 字符串匹配 随机 Comments(0) 2009年6月10日 03:14

随机的快速排序算法

仅仅在原来的快速排序基础上增加了取随机数为划分点，改进了原有快排使用第一个元素作为划分元素的缺点，即减少了遇到最坏情况的可能。

  1. #include<iostream>
  2. #include<time.h>
  3. using namespace std;
  4.  
  5. #define N 20    //  最大数组个数
  6.  
  7. #define MULTIPLIER 0x015A4E35L
  8. #define INCREMENT 1
  9.  
  10. static unsigned long seed;
  11.  
  12. /*      生成随机数种子 */
  13. void random_seed(unsigned long d){
  14.         if(d==0){
  15.                 seed = time(0);
  16.         }else{
  17.                 seed = d;
  18.         }
  19. }
  20.  
  21. /*      生成一个low~high范围内的随机数 */
  22. unsigned int random(unsigned long low, unsigned long high){
  23.         seed = MULTIPLIER * seed + INCREMENT;
  24.         return ((seed>>16)%(high-low)+low);
  25. }
  26.  
  27. /*
  28. * 按枢点元素划分序列
  29. * 输入：数组A[]，序列的起始位置low，终止位置high
  30. * 输出：按枢点元素划分的序列A[]，枢点元素位置i
  31. */
  32. template<class Type>
  33. int split(Type A[], int low, int high){
  34.         int k, i = low;
  35.         Type x= A[low];
  36.         for(k = low+1; k<=high; k++) {
  37.                 if(A[k]<=x){
  38.                         i ++;
  39.                         if(i!=k){
  40.                                 swap(A[i], A[k]);
  41.                         }
  42.                 }
  43.         }
  44.         swap(A[low], A[i]);
  45.         return i;
  46. }
  47.  
  48. /*
  49. * 初始化随机数并执行快排
  50. * 输入：数组A[]，序列的起始位置low，终止位置high
  51. * 输出：排序好的序列A[]
  52. */
  53. template<class Type>
  54. void quicksort_random(Type A[], int low, int high){
  55.         random_seed(0);
  56.         r_quicksort(A, low, high);
  57. }
  58.  
  59. /*
  60. * 随机选择枢点的快速排序
  61. * 输入：数组A[]，序列的起始位置low，终止位置high
  62. * 输出：排序好的序列A[]
  63. */
  64. template<class Type>
  65. void r_quicksort(Type A[], int low, int high){
  66.         int k;
  67.         if( low < high ){
  68.                 k = random(low, high);
  69.                 swap(A[low], A[k]);
  70.                 k = split(A, low, high);
  71.                 r_quicksort(A, low, k-1);
  72.                 r_quicksort(A, k+1, high);
  73.         }
  74. }
  75.  
  76. int main(){
  77.         int A[N];
  78.         int i, n;
  79.  
  80.         cin>>n;
  81.  
  82.         for(i=0; i<n; i++)cin>>A[i];
  83.  
  84.         quicksort_random(A,0,n-1);
  85.  
  86.         for(i=0; i<n-1; i++)cout<<A[i]<<" ";
  87.         cout<<A[n-1]<<endl;
  88.  
  89.         return 0;
  90. }

【算法】与【数据结构】 快速排序 随机 Comments(0) 2009年6月10日 03:12

限界与剪枝求解0/1背包问题

一、 算法思想描述

首先对物体按照价值重量比进行排序。
再从第一个物体开始，对每个物体分两种状态求解：放入与不放入。
在每次求解时都计算该状态可能达到的最优价值，并放入大顶堆中。
当两种状态都求解完后从堆中取出堆顶元素，从该元素所代表的状态中继续进行分支计算。直到深度达到n，问题得到解。

【算法】与【数据结构】 分支限界 01背包 Comments(0) 2009年6月07日 18:20

回溯法求解0/1背包问题

给定背包的载重量M＝20，有6个物体，价值分别为11，8，15，18，12，6，重量分别为5，3，2，10，4，2。利用回溯法求解上述问题。

【算法】与【数据结构】 回溯法 01背包 Comments(0) 2009年5月27日 01:47

回溯法解决马步遍历问题

设计一算法，求解国际象棋中的马的周游问题：给定一8×8的棋盘，马从棋盘的某个位置出发，经过棋盘中的每一个方格恰好一次。（只需求一可行解）

【算法】与【数据结构】 回溯法 马步遍历 Comments(1) 2009年5月27日 01:44

二叉树的非递归遍历

用栈实现即可

【算法】与【数据结构】 数据结构 二叉树 遍历 Comments(0) 2009年5月16日 00:15

动态规划求解01背包问题

令Li,j表示在前j个物体中能够装入载重量为i的背包中的物体的最大价值，i=1,2,…,m。显然，在前j个物体中，能够装入载重量为i的背包中，有些物体可以装入背包，有些物体不能装入背包。于是，可以得到下面的动态规划函数：
L_{0,0} = L_{i,0} = L_{0,i} = 0             1$<=$i$<=$m, 1$<=$j$<=$n
L_{i,j} = $\begin{Bmatrix} L_{i,j-1} & i <$ w_j \\max(L_{i,j-1}, L_{i-w_j, j-1} + p_j) & i>=$ w_j

【算法】与【数据结构】 动态规划 背包问题 Comments(0) 2009年4月29日 08:27

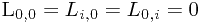
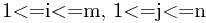
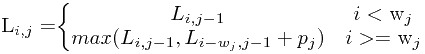
动态规划求解最长公共子序列问题

如果记Ln,m为序列An和Bm的最长公共子序列的长度，则Li,j为序列Ai和Bj的最长公共子序列的长度。根据最长公共子序列的性质，有：L_{0,0} = L_{i,0} = L_{0,i} = 0            1$<=$i$<=$n, 1$<=$j$<=$m
L_{i,j} = $\begin{Bmatrix} L_{i-1,j-1} + 1 & a_i = b_j, i>0 , j>0\\max(L_{i,j-1}, L_{i-1, j}) & a_i $\neq$ b_j, i>0, j>0

【算法】与【数据结构】 动态规划 Comments(0) 2009年4月29日 08:23