Liny_@NotePad

沉迷ACG中

动态规划求解最长公共子序列问题

YOYO posted @ 2009年4月29日 08:23 in 【算法】与【数据结构】 with tags 动态规划 , 4086 阅读

如果记Ln,m为序列An和Bm的最长公共子序列的长度，则Li,j为序列Ai和Bj的最长公共子序列的长度。根据最长公共子序列的性质，有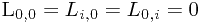：L_{0,0} = L_{i,0} = L_{0,i} = 0            1$<=$i$<=$n, 1$<=$j$<=$m
L_{i,j} = $\begin{Bmatrix} L_{i-1,j-1} + 1 & a_i = b_j, i>0 , j>0\\max(L_{i,j-1}, L_{i-1, j}) & a_i $\neq$ b_j, i>0, j>0

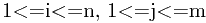
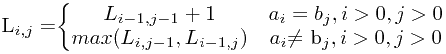
  1. #include<iostream>
  2. using namespace std;
  3.  
  4. #define N 50
  5.  
  6. /*
  7. * 求最长公共子序列算法
  8. *
  9. * 输入：字符串a[]，字符串b[]
  10. * 输出：最长公共子序列c[]及其长度len
  11. */
  12. int lcs(char a[], char b[], char c[]){
  13.         int mz[N+1][N+1],s[N+1][N+1];
  14.         int n, m;
  15.         int i, j, k;
  16.         n = strlen(a), m = strlen(b);
  17.  
  18.         //      初始化
  19.         memset(mz,0, sizeof(mz));
  20.         memset(s, 0, sizeof(s));
  21.  
  22.         //      计算长度
  23.         for(i=1; i<=n; i++){
  24.                 for(j=1; j<=m; j++){
  25.                         if(a[i-1]==b[j-1]){     //   若两个字符相等，则是公共子序列的一部分
  26.                                 mz[i][j] = mz[i-1][j-1]+1;
  27.                         }else{        //        否则 判断哪个是不需要的字符
  28.                                 if(mz[i-1][j]>=mz[i][j-1]){ //若没有a[i]时最长序列大于没有b[j]的
  29.                                         mz[i][j] = mz[i-1][j];
  30.                                         s[i][j] = -1;         // 说明a[i]肯定不在公共子序列中
  31.                                 }else{
  32.                                         mz[i][j] = mz[i][j-1];
  33.                                         s[i][j] = 1;        //  反之，说明b[j]肯定不在公共子序列中
  34.                                 }
  35.                         }
  36.                 }
  37.         }
  38.  
  39.         //      求最长公共子序列字符
  40.         i = n, j = m;
  41.         k = mz[n][m];
  42.  
  43.         c[k--] = '\0';
  44.         while(i>0&&j>0){
  45.                 switch(s[i][j]){
  46.                 case -1:                                //      如果为-1，表示a[i]肯定不在，i--
  47.                         i--;
  48.                         break;
  49.                 case 0:     //       如果它在公共子序列中，直接存入
  50.                         c[k--] = a[i-1];
  51.                         i--, j--;
  52.                         break;
  53.                 case 1:     //       如果为1，表示b[j]肯定不在，j--
  54.                         j--;
  55.                         break;
  56.                 }
  57.         }
  58.  
  59.         return mz[n][m];
  60. }
  61.  
  62. int main(){
  63.         char a[N],b[N],c[N];
  64.         while(cin>>a>>b){
  65.                 int len = lcs(a,b,c);
  66.                 cout<<"最长公共子序列是："<<c<<endl;
  67.                 cout<<"长度为："<<len<<endl;
  68.         }
  69.         return 0;
  70. }


 

Small_feed 评论 (0)

登录 *


loading captcha image...
(输入验证码)
or Ctrl+Enter