动态规划求解01背包问题
令Li,j表示在前j个物体中能够装入载重量为i的背包中的物体的最大价值,i=1,2,…,m。显然,在前j个物体中,能够装入载重量为i的背包中,有些物体可以装入背包,有些物体不能装入背包。于是,可以得到下面的动态规划函数:
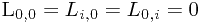
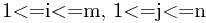
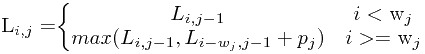
动态规划求解最长公共子序列问题
如果记Ln,m为序列An和Bm的最长公共子序列的长度,则Li,j为序列Ai和Bj的最长公共子序列的长度。根据最长公共子序列的性质,有: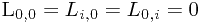
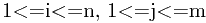
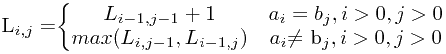
动态规划求解资源最优分配问题
为第i个工程计算最优时,只需将分配若干给前i-1个工程、剩下的留给当前工程得到的各种分配方案,和只分配给当前工程的方案,取其中的最大值即可;而第一个工程解就是只分配给自身的解。
动态规划求多段图单源最短路径
从终点n-1开始,直到顶点0,对每个点:
遍历其所能达到的各个结点,判断通过该结点访问终点的路径是否小于当前能找到的最短距离,是则更新,否则不变。
最后,顶点0找到的最短距离必然是该点到达终点n-1的最短距离。
* 局限性:本程序只能求从顶点0到顶点n-1的最短路,且只能从编号较小的点访问编号较大的点。
