Liny_@NotePad

沉迷ACG中

动态规划求解01背包问题

YOYO posted @ 2009年4月29日 08:27 in 【算法】与【数据结构】 with tags 动态规划 背包问题 , 5128 阅读

令Li,j表示在前j个物体中能够装入载重量为i的背包中的物体的最大价值，i=1,2,…,m。显然，在前j个物体中，能够装入载重量为i的背包中，有些物体可以装入背包，有些物体不能装入背包。于是，可以得到下面的动态规划函数：
L_{0,0} = L_{i,0} = L_{0,i} = 0             1$<=$i$<=$m, 1$<=$j$<=$n
L_{i,j} = $\begin{Bmatrix} L_{i,j-1} & i <$ w_j \\max(L_{i,j-1}, L_{i-w_j, j-1} + p_j) & i>=$ w_j

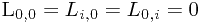
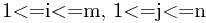
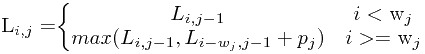
  1. #include<iostream>
  2. using namespace std;
  3.  
  4. #define M 50    //  背包最大载重
  5. #define N 15    //  最多物体个数
  6.  
  7. int p[N+1], w[N+1];
  8. bool x[N+1];
  9. int m, n;
  10.  
  11. int knapsack(){
  12.         int mz[M+1][N+1];
  13.         int i,j;
  14.  
  15.         //      初始化
  16.         memset(mz, 0, sizeof(mz));
  17.         memset(x, false, sizeof(x));
  18.  
  19.         //      DP
  20.         for(i=1; i<=m; i++){
  21.                 for(j=1; j<=n; j++){
  22.                         mz[i][j] = mz[i][j-1];  //        默认为不能放该物体时的最优解
  23.                         if(i>=w[j]&&mz[i-w[j]][j-1]+p[j]>mz[i][j]){     //   如果可以放入且放入更优时
  24.                                 mz[i][j] = mz[i-w[j]][j-1] + p[j];            //    放入
  25.                         }
  26.                 }
  27.         }
  28.  
  29.         //      计算放入背包的物体
  30.         for(i=m, j=n; j>0; j--){
  31.                 if(mz[i][j]>mz[i][j-1]){        //      如果能取该物体时价值大于不能取该物品
  32.                         x[j] = true; i -= w[j]; //       说明该物体被放入了背包
  33.                 }
  34.         }
  35.  
  36.         return mz[m][n];
  37. }
  38.  
  39. int main(){
  40.         int i;
  41.  
  42.         cout<<"请输入物体个数：";
  43.         cin>>n;
  44.  
  45.         cout<<"请输入物体重量：";
  46.         for(i=1; i<=n; i++){
  47.                 cin>>w[i];
  48.         }
  49.  
  50.         cout<<"请输入物体价值：";
  51.         for(i=1; i<=n; i++){
  52.                 cin>>p[i];
  53.         }
  54.  
  55.         cout<<"请输入背包载重量：";
  56.         cin>>m;
  57.  
  58.         cout<<"背包最大价值为"<<knapsack()<<endl;
  59.         cout<<"背包中放入的物体有：";
  60.         for(i=1; i<=n; i++)if(x[i])cout<<i<<" ";
  61.         cout<<endl;
  62.  
  63.         return 0;
  64. }

 

Small_feed 评论 (0)

登录 *


loading captcha image...
(输入验证码)
or Ctrl+Enter