动态规划求解01背包问题
令Li,j表示在前j个物体中能够装入载重量为i的背包中的物体的最大价值,i=1,2,…,m。显然,在前j个物体中,能够装入载重量为i的背包中,有些物体可以装入背包,有些物体不能装入背包。于是,可以得到下面的动态规划函数:
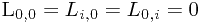
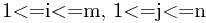
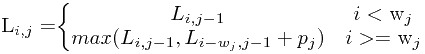
贪心法:部分背包问题
因可以取物体的部分放入,故每次选择价值重量比最高的物体放入,可保证放入的价值一定最大,满足贪婪选择性质和最有子结构性质,故采用贪心算法求解:
1. 根据各个物体的价值p与重量w计算价值重量比v
2. 根据v降序排序
3. 从当前最大的v的开始,判断该物体重量是否超过背包剩余载重
4. 是则放入背包剩余载重量的物体,加上这部分的价值,跳到7
5. 否则将物体完整放入背包,加上物体的价值
6. 若还有物体未放入背包,则跳到3
7. 输出背包中物体的总价值
